Algebra Lineare
Strutture Algebriche
- Insieme: collezione di un elementi che hanno tutti una stessa caratteristica
- Funzione: dati due insiemi e , si dice (funzione) una legge che associa ad ogni elemento di uno di . Spiegazione approfondita delle funzioni si legge ” definita in a valori in “.
Matrici
Matrice: una matrice è una tabella di m-righe e n-colonne, ogni singola “cella” di questa matrice si chiama entrata. Una matrice con lo stesso numeri di righe e di colonne si dice quadrata, queste tipo di matrici possono assumere varie forme:
- Triangolare diagonale: se sopra e sotto la diagonale principale ci sono tutti zero.
- Triangolare superiore: se sotto la diagonale principale ci sono tutti zero.
- Triangolare inferiore: se sopra la diagonale principale ci sono tutti zero. Una qualsiasi matrice si può dire:
- Simmetrica: se la matrice è uguale alla sua trasposta.
- Antisimmetrica: se la matrice è uguale all’opposta della sua trasposta.
Matrice trasposta: Ipotizzando una matrice A dove ogni entrata è definita come la matrice trasposta di A la matrice trasposta di A che denotiamo con con le entrate definite così:
 Per trasporre una matrice basta scrivere le sue righe sotto forma di colonne. Il determinante di A è uguale a determinante di
Per trasporre una matrice basta scrivere le sue righe sotto forma di colonne. Il determinante di A è uguale a determinante di
Matrici equivalenti: 2 matrici sono uguali se ogni singola entrate è uguale in entrambe le matrici
Operazioni tra matrici
Somma tra matrici: per sommare 2 matrici quest’ultime devono avere le stesse dimensioni
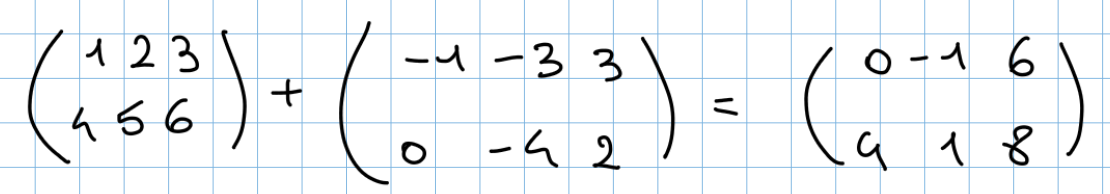 Moltiplicazioni tra un numero e una matrice: il numero per la quale moltiplichiamo la matrice viene detto scalare (nell’esempio sottostante lo scalare si chiama c)
Moltiplicazioni tra un numero e una matrice: il numero per la quale moltiplichiamo la matrice viene detto scalare (nell’esempio sottostante lo scalare si chiama c)
 Sottrazione tra matrici: per poter fare la differenza tra 2 matrici devo avere lo stesso numero di righe e di colonne in entrambe le matrici
Moltiplicazioni tra matrici: date 2 matrici A e B per poter fare la moltiplicazione tra queste deve essere vera almeno una delle 2 condizioni sottostanti:
Sottrazione tra matrici: per poter fare la differenza tra 2 matrici devo avere lo stesso numero di righe e di colonne in entrambe le matrici
Moltiplicazioni tra matrici: date 2 matrici A e B per poter fare la moltiplicazione tra queste deve essere vera almeno una delle 2 condizioni sottostanti:
- numero di colonne di A = numero di righe di B
- numero di colonne di B = numero di righe di A
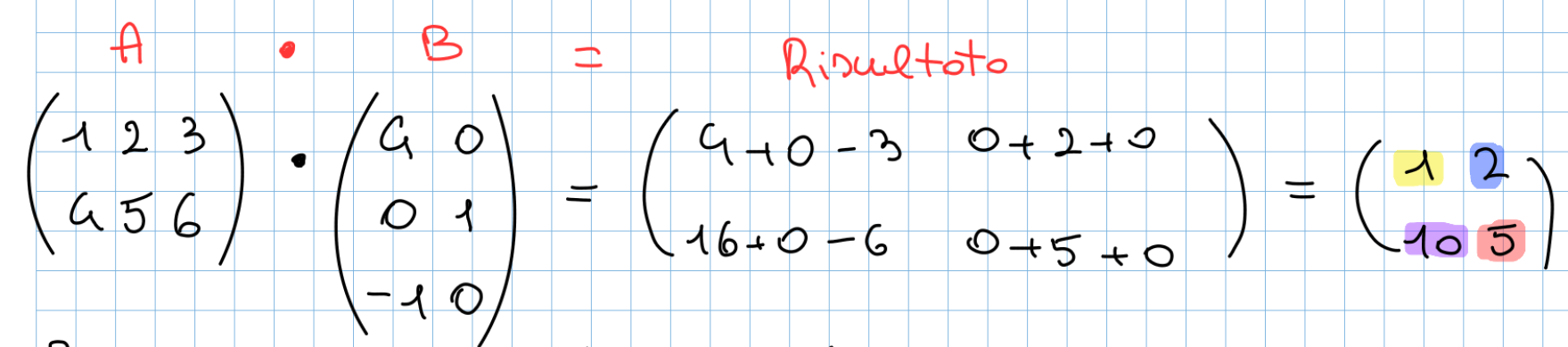 Ogni entrata della matrice “Risultato” è il risultato di una moltiplicazione tra una riga della prima matrice e una colonna della seconda. Di seguito il calcolo dell’entrata in posizione 1,1 della matrice “Risultato”:
Ogni entrata della matrice “Risultato” è il risultato di una moltiplicazione tra una riga della prima matrice e una colonna della seconda. Di seguito il calcolo dell’entrata in posizione 1,1 della matrice “Risultato”:
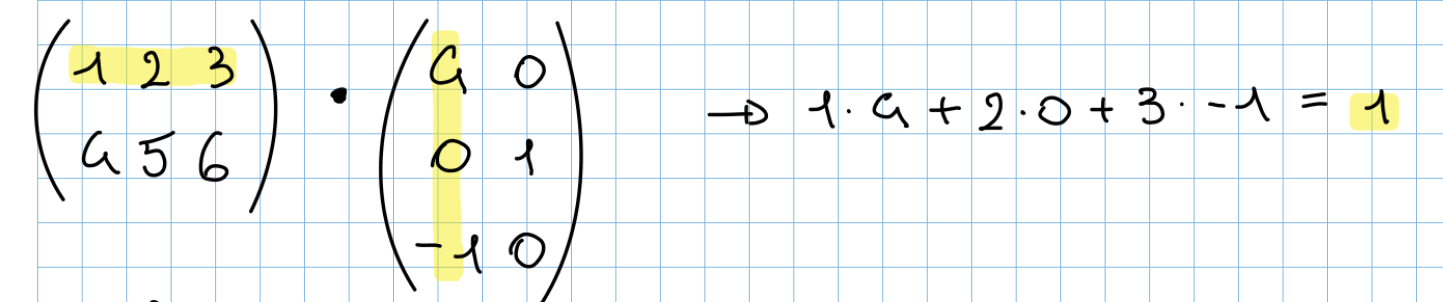
Matrice identità: denotiamo la matrice identità come . Definiamo matrice identità la matrice che rende vera questa cosa:
- La matrice identità è una matrice quadrata che segue questa forma:
Forma di echelon: una matrice si dice in forma di echelon se:
- Se tutte le righe nulle sono in fondo
- Se in ogni riga il primo elemento (detto pivot) partendo da sinistra si trova alla destra di tutti i pivot delle righe superiori e ha tutti zero sotto
 Forma di echelon ridotta: una matrice si dice in forma di echelon ridotta se:
Forma di echelon ridotta: una matrice si dice in forma di echelon ridotta se: - É in forma di echelon normale
- tutti i pivot sono uguali ad 1
- ogni pivot è l’unico elemento non zero della sua colonna
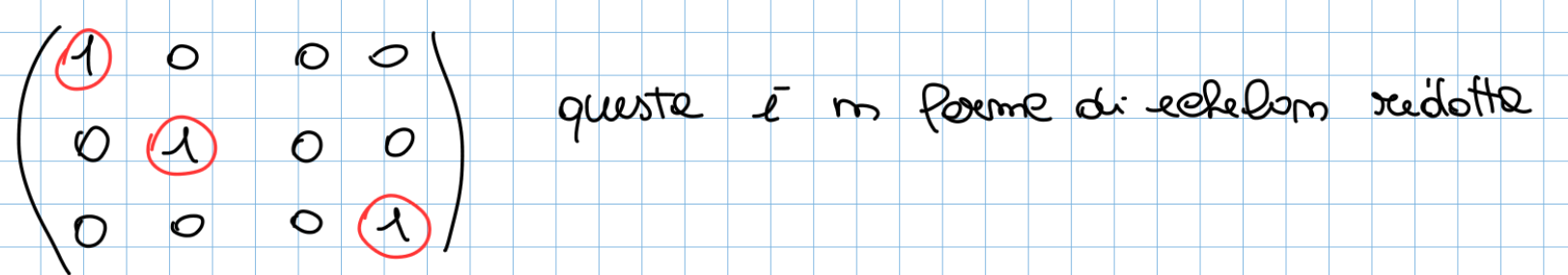
😍Metodo di Gauss-Jordan:😍 Questo metodo viene usato per trasformare qualsiasi matrice in forma di echelon ridotta, Spiegazione di come funziona (farò riferimento a questa tecnica con la notazione G-J).
Rango: il rango di una matrice è il numero di pivot nella sua forma di echelon ridotta, il rango della matrice A lo denotiamo con , questo numero rispetta sempre questa condizione: - Il rango di una matrice è massimo
Invertibilità delle matrici: una matrice si dice invertibile se il suo rango è massimo, denotiamo l’inversa della matrice con Inversa di una matrice: Data una matrice A per trovare la sua inversa seguo questi step:
- Controllo se il suo rango è massimo
- Creo una nuova matrice unendo la matrice A e la matrice identità
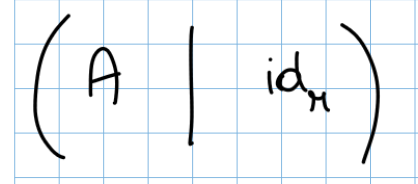
- Faccio Gauss-Jordan su questa matrice e ottengo una matrice di questo tipo
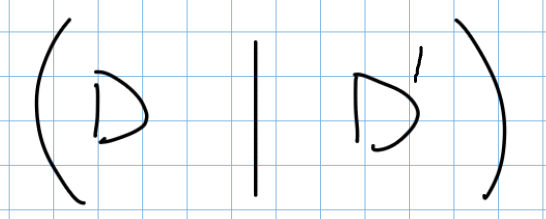
- Se allora
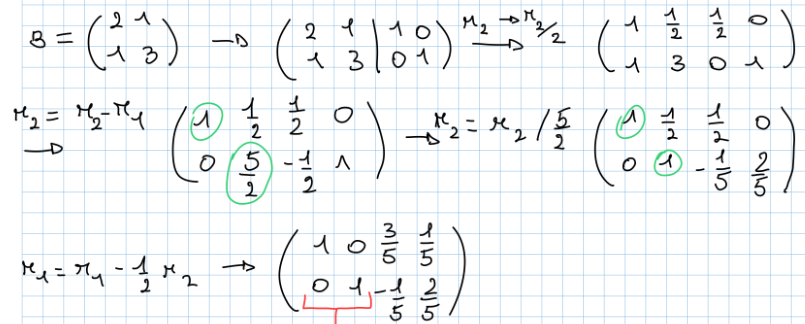 Essendo allora
Essendo allora
Sottomatrici: Sia con . La sottomatrice di A è una matrice ottenuta rimuovendo le i-esime e le j-esime colonne e righe.
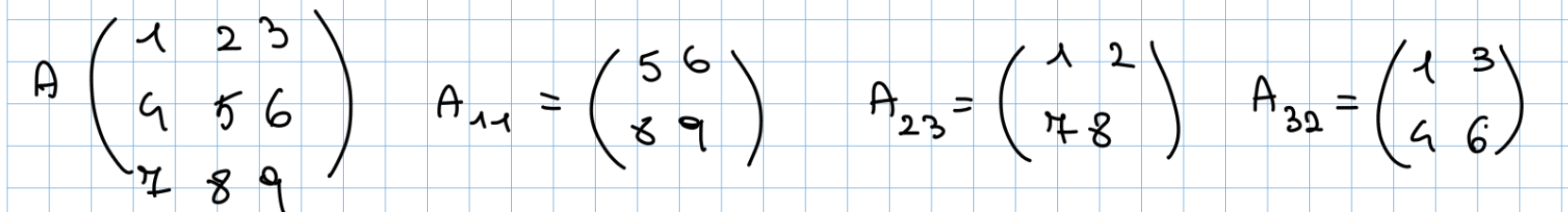
Minore: Il termine “minore” in algebra lineare si riferisce a una sottomatrice di una matrice più grande. Più precisamente, il minore di una matrice è il determinante di una sottomatrice ottenuta rimuovendo una o più righe e colonne dalla matrice originale.
Determinante: è numero associato ad ogni matrice che può dirci molto sulle proprietà della matrice stessa.
Metodo di Sarrus per il calcolo del determinante nelle matrici quadrate che consiste nei seguenti passaggi:
- Prendi la tua matrice normale

- Riscrivi le prime 2 colonne e tracci le diagonali
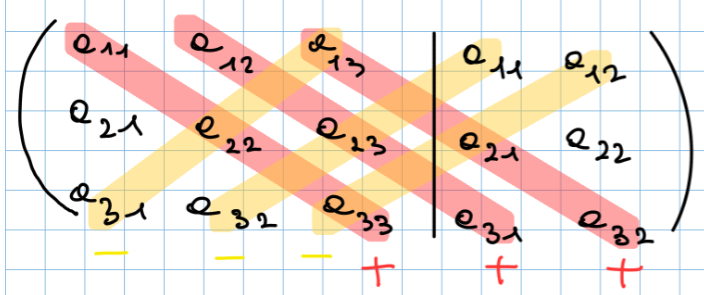
- Faccio le moltiplicazioni delle diagonali, moltiplicando tutto per + nelle diagonali principali e per - nelle diagonali secondarie
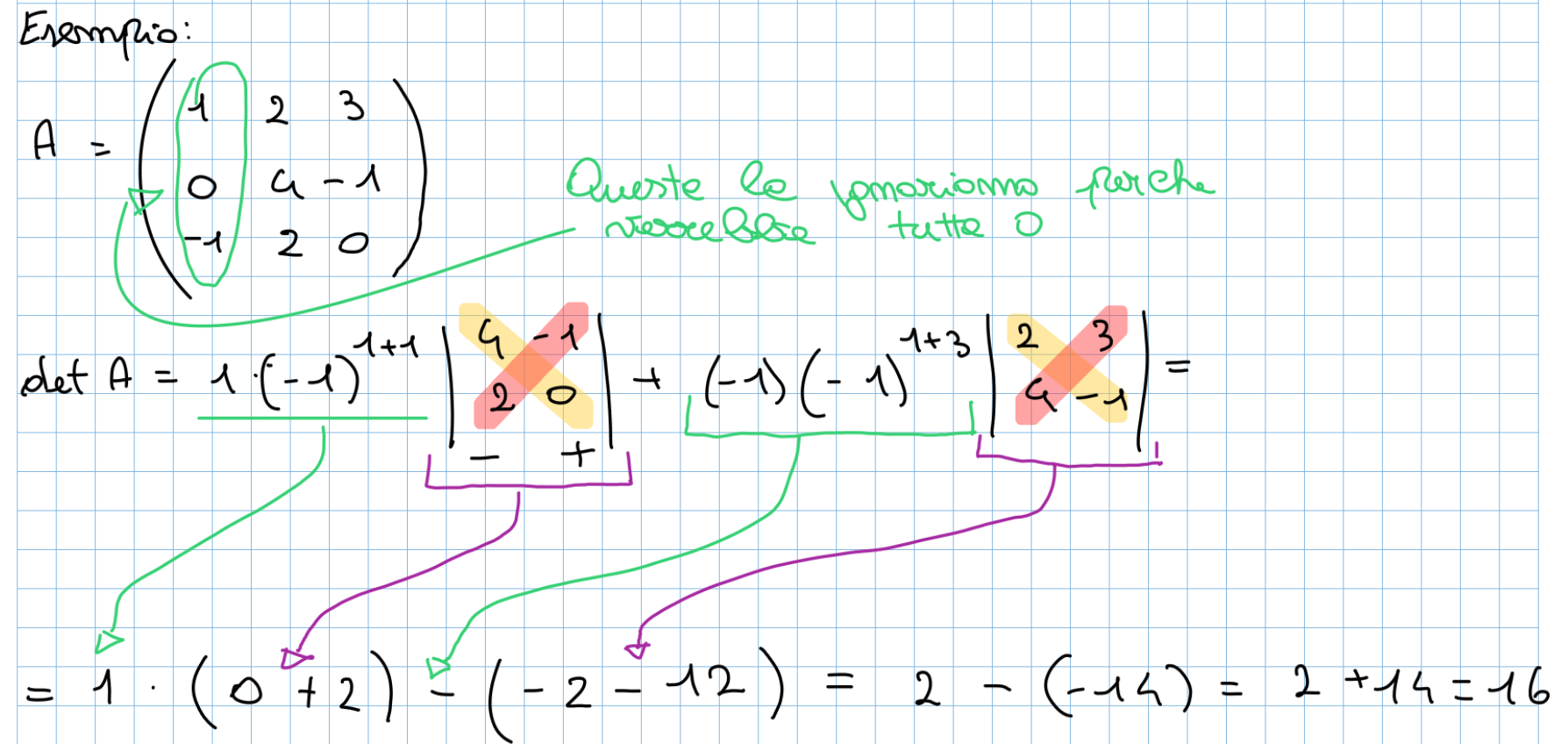
Metodo di Laplace per il calcolo del determinante : questa metodologia si basa su questa formula:
- meno generalizzata diventa: Dove:
- A è la matrice .
- i è l’indice della riga scelta per lo sviluppo.
- è l’elemento della matrice A alla posizione .
- è il minore ottenuto eliminando la riga i e la colonna j dalla matrice A.
Teorema di Binet: se abbiamo 2 matrici quadrate A,B il Dimostrazione???
Teorema degli orlati: Data una matrice A e una sottomatrice quadrata di detta , con dimensioni se tutte le sotto matrici di A di dimensione ottenute orlando hanno allora (orlare una matrice consiste nell’aggiungere una riga o una colonna scelte arbitrariamente dalla matrice padre). Di seguito un’esempio con la seguente matrice:

- Scegliamo una matrice con det 0
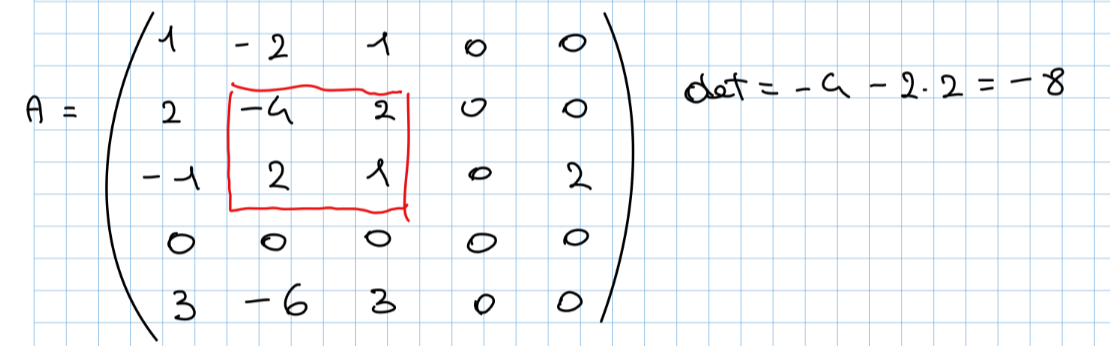
- Alla matrice scelta aggiungiamo una riga ed una colonna scelte in modo casuale e ci calcoliamo il det
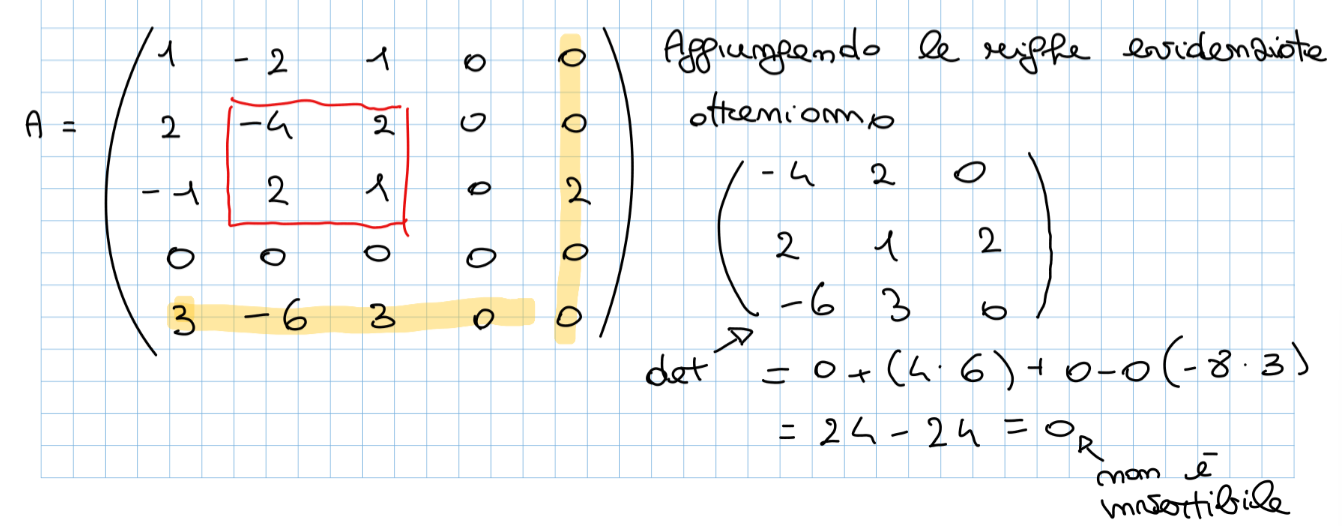
- Aggiungiamo la riga 5 e la colonna 1 e calcoliamo il det
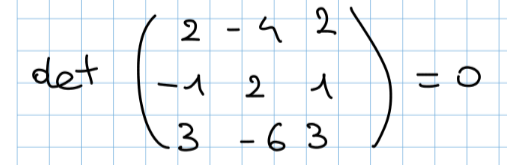
- Continuando e provando notiamo che tutti i determinanti vengono uguali a 0 quindi il
- Teorema Matrici Invertibili dice che: - a) una matrice A è invertibile - b) se allora la matrice inversa è: - c) se è invertibile allora - d)
Sistemi Lineari
Sistema Lineare: è un sistema di equazioni a più incognite (sempre di grado 1) per risolvere un sistema lineare possiamo trasformarlo in una matrice, la matrice che ne esce avrà questa forma: (questa è la definizione della matrice associata al sistema lineare)
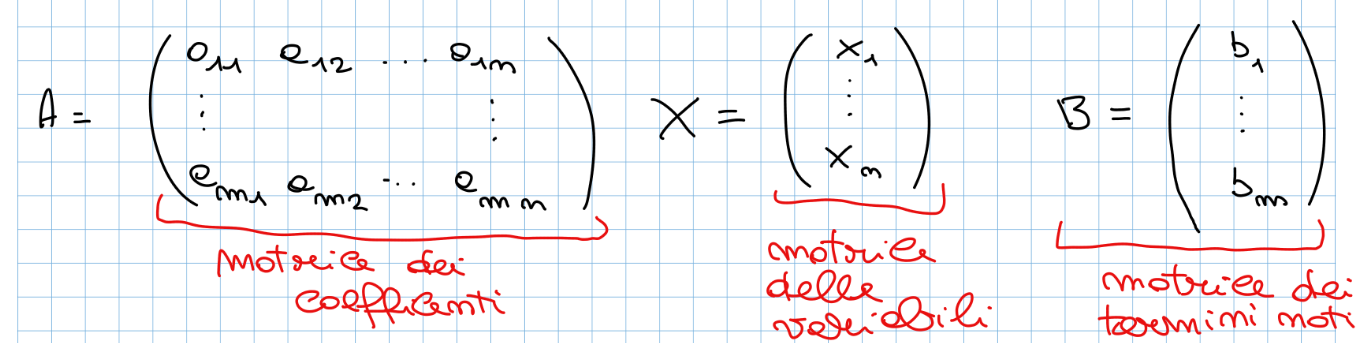 Per risolvere un generico sistema lineare possiamo applicare Gauss-Jordan alla matrice completa che ha questa forma:
Per risolvere un generico sistema lineare possiamo applicare Gauss-Jordan alla matrice completa che ha questa forma:
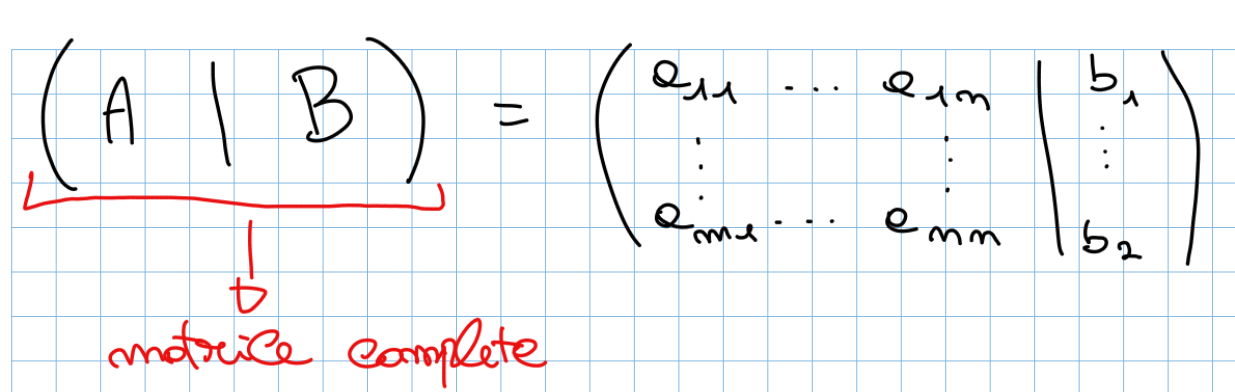 i valori rimasti nella matrice A quando arriviamo in forma di echelon ridotta rappresentano i coefficienti delle incognite, i valori rimasti nella matrice B sono i valori delle incognite.
i valori rimasti nella matrice A quando arriviamo in forma di echelon ridotta rappresentano i coefficienti delle incognite, i valori rimasti nella matrice B sono i valori delle incognite.
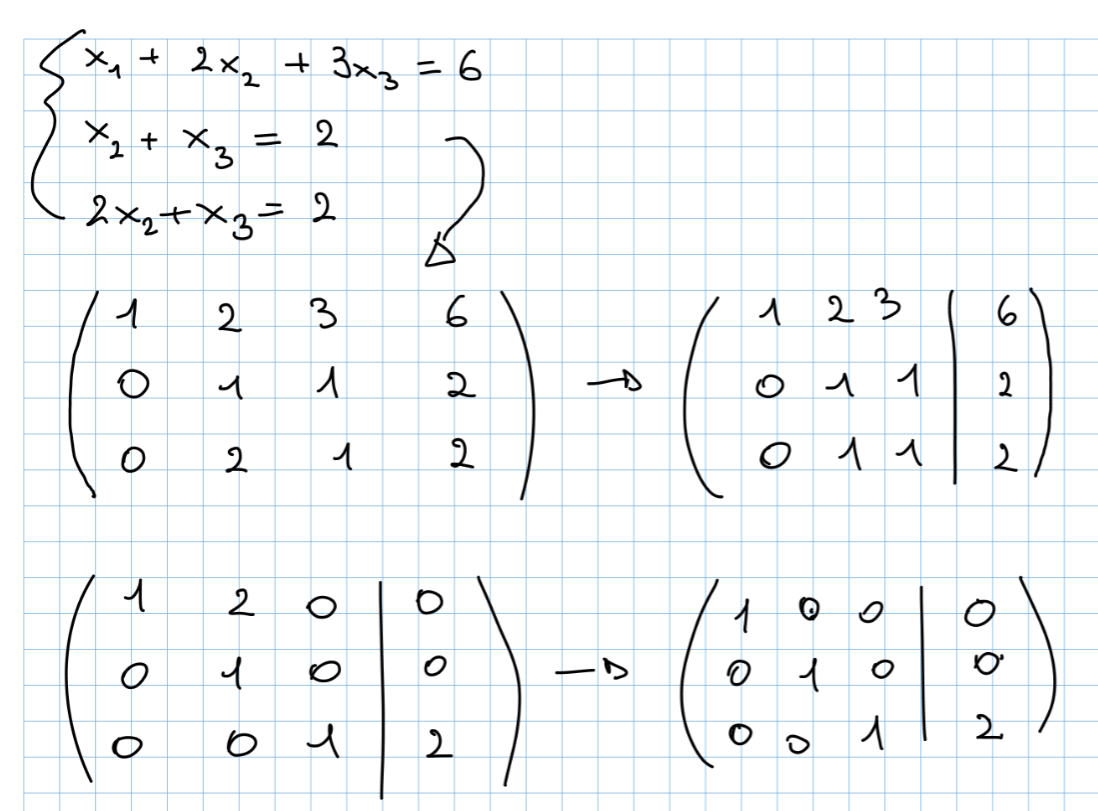 Come possiamo notare da questa immagine facciamo quanto detto prima, le soluzioni che troviamo nella forma finale sono usando questo metodo la risoluzione di un sistema lineare diventa banale.
Ci sono dei casi speciali in cui si può incappare quando si risolvono i sistemi lineari come quelli di seguito:
Come possiamo notare da questa immagine facciamo quanto detto prima, le soluzioni che troviamo nella forma finale sono usando questo metodo la risoluzione di un sistema lineare diventa banale.
Ci sono dei casi speciali in cui si può incappare quando si risolvono i sistemi lineari come quelli di seguito:
- Sistema impossibile: in uno dei passaggi di G-J siamo arrivati a questo punto (vedi immagine sotto), come possiamo notare le soluzioni dell’ultima riga sarebbero , e quindi che questa è chiaramente un’affermazione falsa quindi la risultato del sistema è impossibile da calcolare
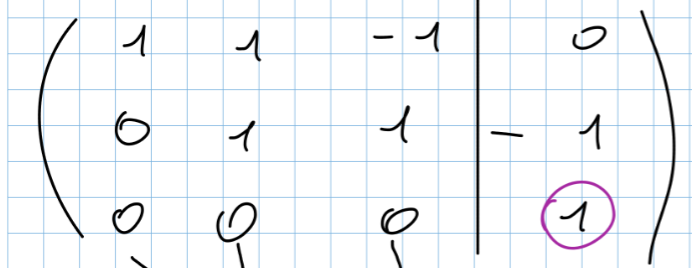
- Sistema con infinite soluzioni: Arrivati al punto di prendere le soluzioni ci siamo resi conto che dipende dal valore di e proprio quest’ultima non ha un valore definito, in questo caso si dice che le soluzioni del sistema sono infinite perché dipendono da un parametro, in questo caso (nelle soluzioni viene posto = )
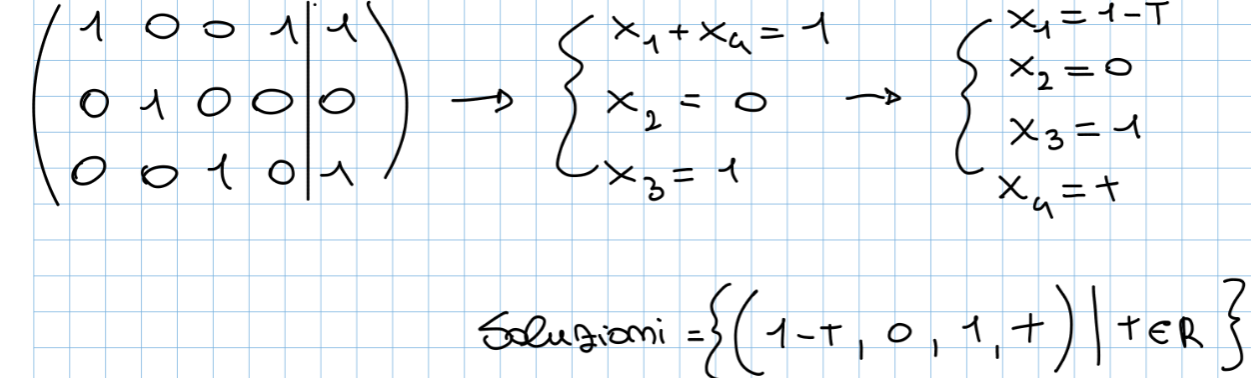
Teorema di Rouchè Capelli: Il sistema con variabili e equazioni ha soluzione se da qui si sviluppano 2 casi:
- se r == n allora il sistema lineare ammette una sola soluzione
- se r < n allora esistono infinite soluzione che dipendono da parametri
Sistemi lineari con parametro : può succedere che in un’esercizio venga inserito un parametro la risoluzione non cambia da un normale sistema lineare dobbiamo solo fare attenzione a questo valore, questo implica che dobbiamo fare di tutto per evitare che sia un pivot, se è un pivot dobbiamo discutere le varie soluzione della matrice al variare del suo valore
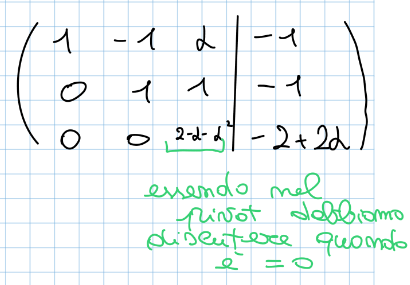
Il nostro obbiettivo per continuare con G-J è quello di far diventare il pivot 1, per fare ciò dobbiamo essere sicuro che il valore di sia diverso da zero, quindi vediamo quando è zero in questo modo: Da questo capiamo che i casi da discutere sono 3:
-
Di seguito il continuo dell’esercizio
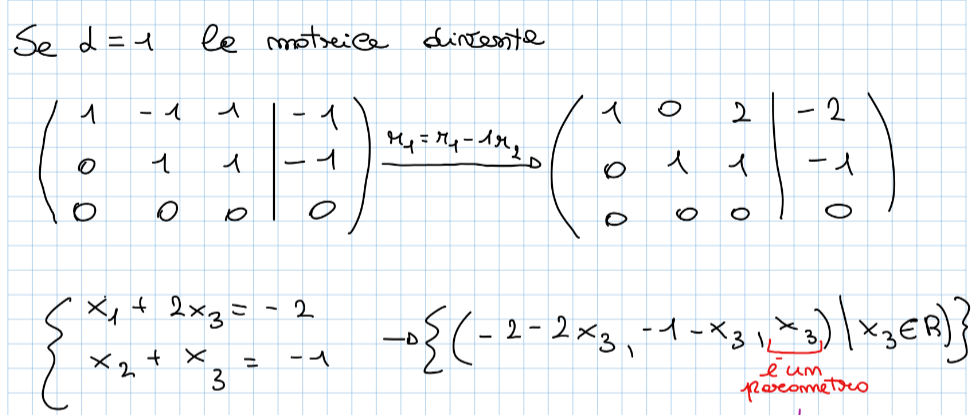
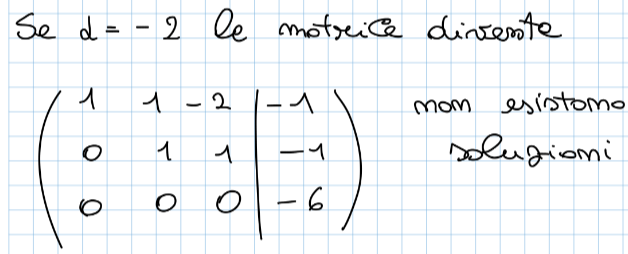
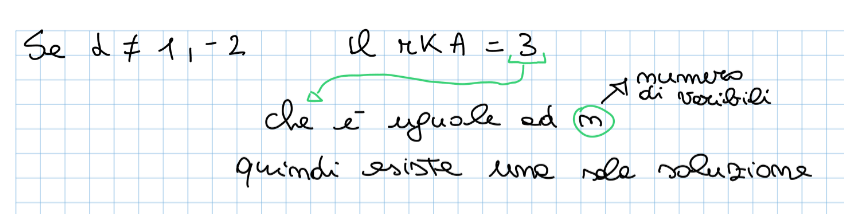 Nell’ultimo caso si vede un’applicazione del teorema di Rouchè Capelli (si lascia al lettore il brivido della scoperta delle soluzioni di quest’ultima matrice 😉)
Nell’ultimo caso si vede un’applicazione del teorema di Rouchè Capelli (si lascia al lettore il brivido della scoperta delle soluzioni di quest’ultima matrice 😉)
Sistemi omogenei: un sistema omogeneo è un sistema lineare che si basa su questo paradigma: e che quindi la matrice B dei termini noti è una matrice nulla (con tutti 0), la risoluzione di questo tipo di sistema lineare non differisce con un sistema lineare normale.
Teorema di Cramer: Per trovare le soluzioni di un sistema lineare del tipo con ovvero un sistema detto determinato (ammette una e una sola () soluzione). Calcoliamo l’unica soluzione delle incognite in questo modo:
- dove è il numero di incognite
- si calcola sostituendo la colonna di con .
- si calcola sostituendo la colonna di con .
- si calcola sostituendo la colonna di con .
Esempio di come trovare le soluzioni di un sistema lineare usando Cramer
 Dimostrazione: prendo quello che devo dimostrare è che A è uguale a B se e soltanto se moltiplicata per quella x quindi seguo i seguenti passi:
Dimostrazione: prendo quello che devo dimostrare è che A è uguale a B se e soltanto se moltiplicata per quella x quindi seguo i seguenti passi:
- Sostituisco ad della prima formula e quindi diventa:
- Sposto le parantesi:
- Per definizione di matrice inversa
- Quindi l’espressione diventa
Spazi Vettoriali
Spazio Vettoriale: si dice spazio vettoriale un insieme su cui valgono le seguenti proprietà:
- è un insieme non vuoto con un’operazione di somma tale che:
- È chiuso rispetto alla somma: .
- La somma è associativa: .
- La somma è commutativa: .
- Esiste un elemento neutro tale che .
- Ogni elemento ha un opposto tale che .
- ha un’operazione di prodotto scalare con un campo (ad esempio, i numeri reali ):
- È chiuso rispetto al prodotto scalare: .
- Vale la distributività rispetto alla somma degli scalari: .
- Vale la distributività rispetto alla somma dei vettori: .
- Vale la compatibilità tra prodotto scalare e moltiplicazione scalare: .
- Il numero (scalare unitario) agisce come identità: . Ipotizzando un insieme sulla quale valgono tutte queste proprietà lo chiamiamo spazio vettoriale, gli elementi di si chiamano vettori.
= { (, ,…, )| }
è uno spazio vettoriale formato dai vettori con al massimo volte , ad esempio , possiamo affermare che questo è uno spazio vettoriale perché valgono tutte le proprietà prima descritte.
Combinazione lineare: un vettore è combinazione lineare degli altri vettori dello spazio vettoriale se esistono dei tale che
Sottospazio: è sottospazio di se e se rispetta queste proprietà:
- Nei sottospazi vettoriali definiamo 2 operazioni:
- Intersezione tra sottospazi: è sempre un sottospazio
- Unione tra sottospazi: è sottospazio solo se uno dei due è sottoinsieme dell’altro (ovvio)
- Somma diretta: Definiamo somma diretta la somma tra 2 sottospazi se e solo se la loro intersezione è ovvero un’insieme con solo lo 0 dentro, questo ci indica che i 2 insiemi sono completamenti diversi.
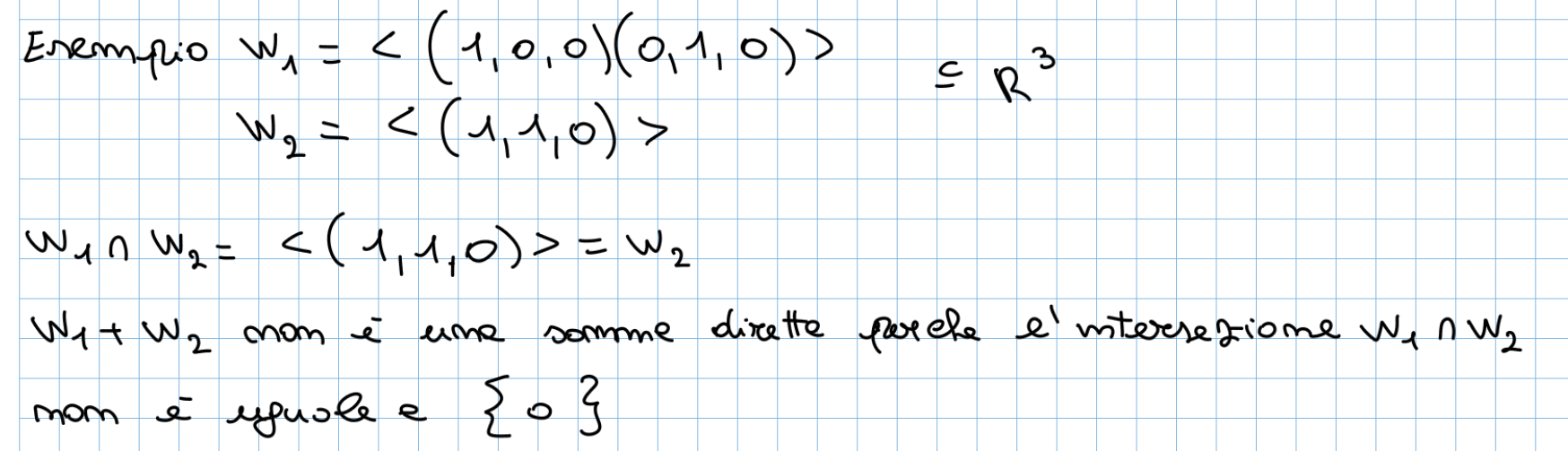
Insieme di Generatori: dato uno spazio vettoriale , un insieme è detto insieme di generatori (indicato con ) se preso un qualunque vettore esso si può scrivere come combinazione lineare (C.L.) dei vettori di .
Linearmente Indipendenti: i vettori si dicono linearmente indipendenti se facendo la combinazione lineare di quest’ultimi l’unico modo per farla venire uguale a 0 è usando dei
Linearmente dipendente: i vettori si dicono linearmente dipendenti se facendo la combinazione lineare di quest’ultimi per un generico il risultato è uguale a
Come capire se uno spazio vettoriale è linearmente indipendente
Per capire se i vettori di uno spazio vettoriale sono linearmente indipendenti creo una matrice con quest’ultimi e mi calcolo il rango:
- Se il rango è massimo allora lo spazio vettoriale è linearmente indipendente
- Se il rango non è massimo vuol dire che qualche vettore può essere scritto come combinazione lineare degli altri e quindi che è linearmente dipendente
Base di uno spazio vettoriale: un insieme è detto Base di se genera e soprattutto se è linearmente indipendente
- è una base di questo perché genera ed è linearmente indipendente
Una base che useremo spesso è la base di anche detta base standard è si presenta in questa forma: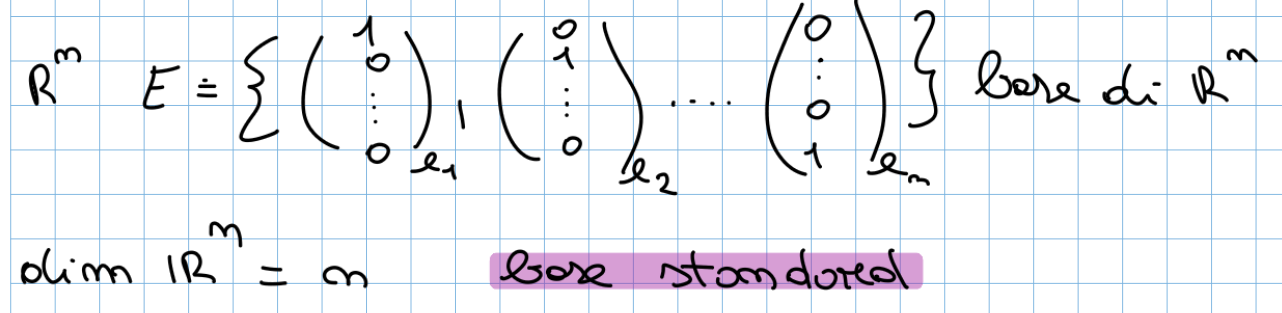
Dimensione di uno spazio vettoriale: la dimensione di uno spazio vettoriale ci indica il numero di vettori che compongono una sua base. V spazio vettoriale, W sottospazio vettoriale di V allora sempre tranne quando
Formula di Grossmann: spazio vettoriale allora
==Lemma di Steinitz: tutte le basi di uno spazio vettoriale hanno la stessa dimensione==
Per rappresentare la base di sottospazio abbiamo 2 metodi:
- Forma parametrica: ovvero come spazio generato da un insieme di vettori:
 Di seguito un’esempio:
Di seguito un’esempio:
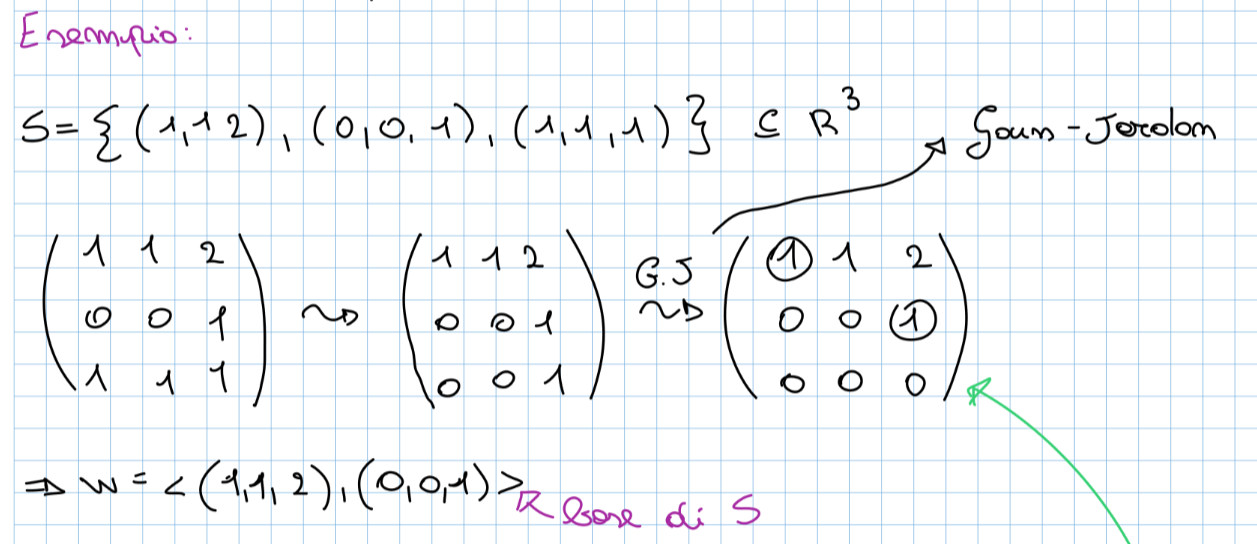
- Forma cartesiana: come soluzione di un sistema lineare omogeneo
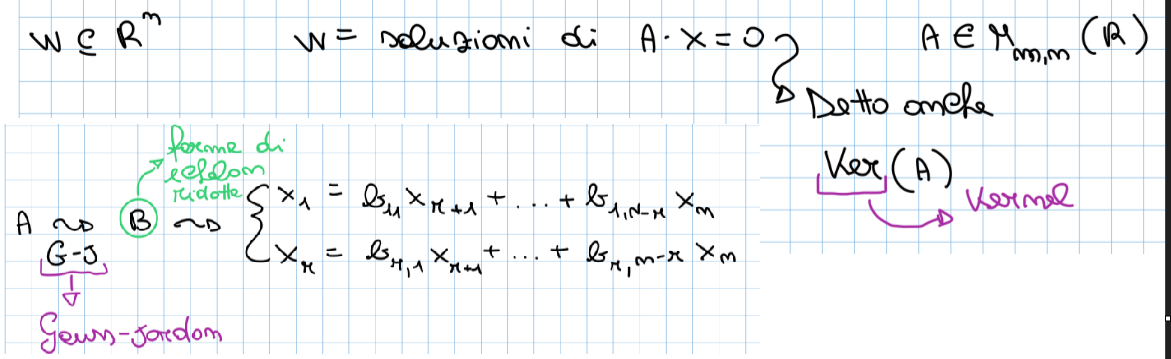 Di seguito un’esempio:
Di seguito un’esempio:

Come passiamo da una rappresentazione ad un’altra?
- Forma cartesiana → forma parametrica
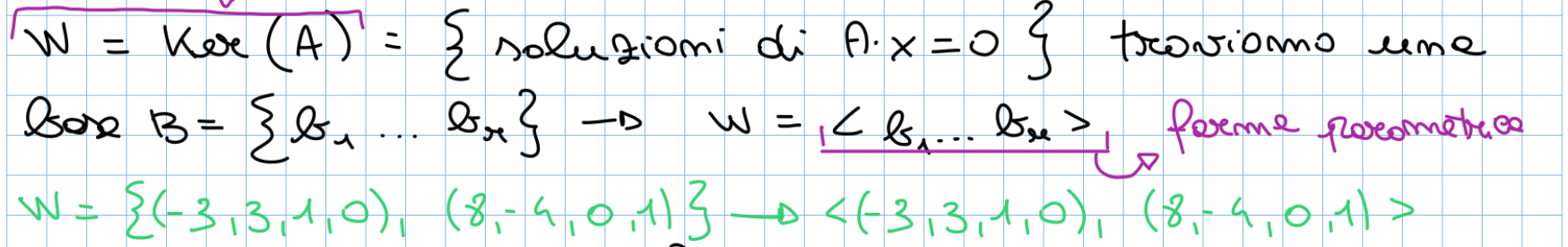
- Forma parametrica → forma cartesiana
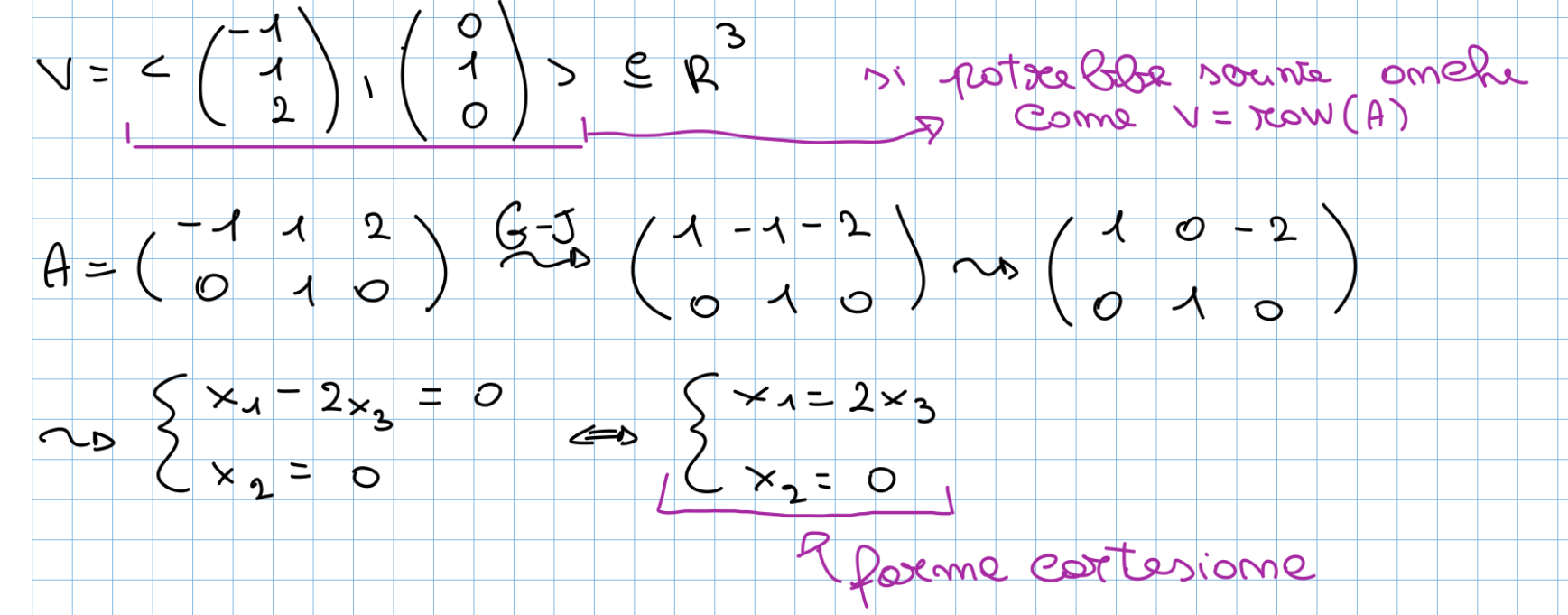 Passare da una forma all’altra è utile per le operazioni che dobbiamo andare a fare, se dobbiamo fare un’intersezione di sottospazi la forma cartesiana risulta più comoda, invece per la somma di sottospazi la parametrica è la più comoda.
Passare da una forma all’altra è utile per le operazioni che dobbiamo andare a fare, se dobbiamo fare un’intersezione di sottospazi la forma cartesiana risulta più comoda, invece per la somma di sottospazi la parametrica è la più comoda.
Teorema del rango: Data una matrice con dimensioni possiamo definire il seguente teorema:
opzionalmente si fa riferimento alla dimensione del indicandolo con di conseguenza la formula diventa:
Applicazioni Lineari
-
Applicazione Lineare: corrispondenza (funzione) tra due K-spazi vettoriali.
-
Immagine (): insieme del codominio formato dai vettori immagine dei vettori del dominio. - L’immagine è sottospazio del codominio, si dimostra (4*. L13) provando che è chiusa rispetto alla somma e al prodotto esterno. - Studio - - Base: vettori L.I. di V (gli stessi che formano il rango) - Equazione Cartesiana: metodo matrice Z (si mettono in riga i vettori base, nell’ultima riga le incognite, si calcola il determinante)
-
Nucleo (): insieme del dominio formato dai vettori che hanno come immagine il vettore nullo. - Il nucleo è sottospazio del dominio, si dimostra (5*, L14) provando che è chiusa rispetto alla somma e al prodotto esterno esterno. - Studio - - Base: - Equazioni Cartesiane: ricavate dal sistema precedente (o metodo matrice Z)
-
Iniettività: una funzione si dice iniettiva se presi due qualsiasi vettori del dominio diversi allora ne deve seguire che le loro immagini siano diverse.
-
Suriettività: una funzione si dice suriettiva se ogni vettore del codominio è raggiunto da almeno un vettore del dominio.
-
Teorema sul Nucleo e Iniettività: afferma che è iniettiva - Dimostrazione (6*, L14)
-
Applicazione Identica: applicazione lineare cui legge corrisponde a
-
Applicazione Inversa: Date due applicazioni lineari e se e allora è invertibile e è detta applicazione inversa di . - e devono essere suriettive e iniettive. ---
Endomorfismi
- Endomorfismo: applicazione lineare dove dominio codominio.
- Isomorfismo: un’applicazione lineare biettiva (iniettiva e suriettiva), quindi necessariamente endomorfismo.
- Autovalore: dato un endomorfismo , si dice autovalore se esiste un vettore con tale che .
- Autovettore: dato un endomorfismo , , si dice autovettore se esiste un tale che .
- Autospazio: dato un endomorfismo , si dice autospazio il sottospazio di V definito nel modo seguente:
- Polinomio Caratteristico: data una matrice il .
- Molteplicità Algebrica: per molteplicità algebrica di si intende il numero di volte in cui è soluzione del polinomio caratteristico.
- Molteplicità Geometrica: per molteplicità geometrica di si intende la dimensione dell’autospazio .
- Endomorfismo Associato all’Autovalore: indichiamo con l’endomorfismo associato all’autovalore .
- Teorema sulle Molteplicità: dato un endomorfismo e un autovalore allora .
- Endomorfismo Semplice: un endomorfismo si dice semplice se esiste una base formata interamente da autovettori.
- Matrici simili: due matrici e si dicono simili se .
- Teorema sulla diagonalizzazione: una matrice è diagonalizzabile è semplice oppure se è simile a una matrice diagonale. - Matrice Diagonalizzata: matrice che ha sulla diagonale principale le molteplicità algebriche degli autovalori. - Matrice Diagonalizzante: matrice che ha in colonna una base degli autovettori.
- Teorema Autospazio: sia un K-spazio vettoriale e un endormofismo. Allora ne segue che . - Dimostrazione (7*, L19): si usa la definizione dell’autospazio. ---